Метод анализа структуры конечных множеств объектов путем расчета матриц бинарного сходства объектов в многомерном пространстве альтернативных признаков с учетом информативности этих признаков

А.В. Галанин © 2010

© OCR - А.В. Галанин, 2010. Воспроизводится по тексту: Галанин А.В. Эколого-ценотическая информативность видов и измерение флористического сходства растительных сообществ // Флористические критерии при классификации растительности. Уфа: Башк. филиал АН СССР, 1981.

 

 

Бинарное или попарное сравнение объектов ( n 1 , n 2 , n 3 …. n m ) некоторого множества N в многомерном пространстве признаков ( a 1 , a 2 , a 3 , … a k ), когда значение каждого признака для каждого объекта может принимать только два значения (0 или 1), т.е. определяется альтернативно, производится с учетом информативности каждого признака. Исходные данные представлены в виде прямоугольной матрицы размером NxA . В этой матрице не должно быть строк и столбцов, которые содержат только значения 0, или только значения 1. В каждой строке и в каждом столбце должны быть как значения 0, так и значения 1.

Для каждого признака рассчитывается его встречаемость в данной матрице. Она определяется как отношение количества объектов, имеющих по данному признаку значения 1 к общему количеству объектов в данной матрице. Так определяется частота каждого признака в матрице. Частота признака изменяется от 0 до 1, но признаки, имеющие в данной матрице только значения 0 или только значения 1 при дальнейшей работе из матрицы должны быть исключены.

Частота значения «1) признака А в матрице используется для расчета его информативности в данной матрице. Информативность рассчитывается по формуле:

I A 1 = - log P A 1 ,

где: . P A 1 = N 1 / N ; P A 1 – вероятность значения «1» признака А в данной матрице; N 1 – количество объектов в данной матрице, имеющих значение «1»; N – общее количество объектов в данной матрице NxA . Вероятность нулевого значения признака А может быть рассчитана по формуле: P A 0 = 1 - N 1 / N ., а информативность нулевого значения признака А в данной матрице можно рассчитать по формуле:

I A0 = - log P A0 = - log (1 - N 1 /N).

Обычное бинарное сходство объектов рассчитывается по формуле Жаккара:

К ж = в/С + Р – в,

Где: в – количество признаков в матрице, по которым данная пара объектов имеет совпадающие значения «1», С – количество признаков в матрице, по которым первый объект имеет значения «1», Р - количество признаков в матрице, по которым второй объект имеет значения «1».

 

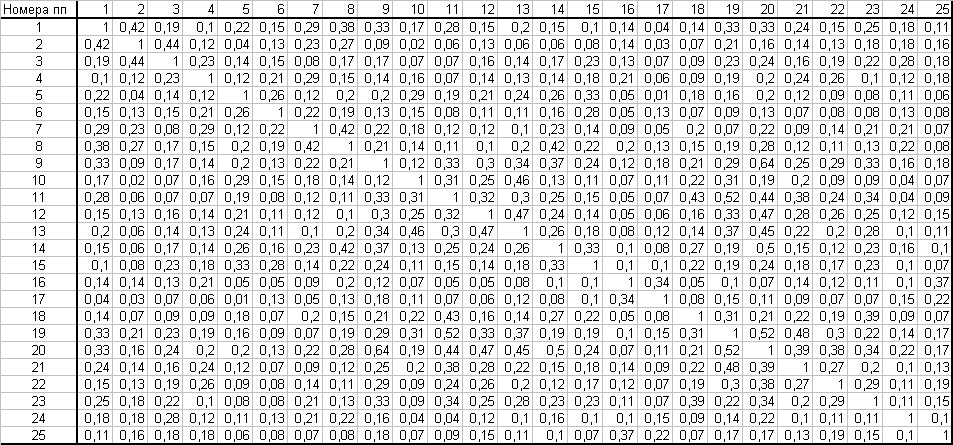
Бинарное сходство объектов с учетом информативности положительных значений признаков в матрице можно рассчитать используя формулу Жаккара, но вместо значения в, С и Р, подставляя соответствующие суммы информативностей этих совокупностей признаков. В результате бинарного сравнения объектов с учетом информативности положительных значений признаков в матрице мы получаем квадратную матрицу бинарных значений размером MxM . Таким образом, можно попарно сравнивать между собой описания растительности пробных площадей, составленных в определенном ландшафтном районе, описания площадок, заложенных в пределах одной пробной площади. Этим методом можно анализировать множество видов в пространстве альтернативных морфологических признаков и другие многомерные объекты. Следует помнить, что больший вес при расчете бинарного сходства объектов с учетом информативности положительных значений признаков имеют признаки с меньшей вероятностью, т.е. признаки редкие. Частые признаки при расчете такого сходства имеют меньший вес. В ряде случаев такое различение признаков при расчете бинарного сходства объектов бывает просто необходимо. Использование метода бинарного информационного сходства при сравнении геоботанических описаний показало, что этот метод имеет большую разрешающую способность, он позволяет более тонко анализировать как внутриландшафтное разнообразие растительности, так и разнообразие растительности на ценотическом уровне ее организации.   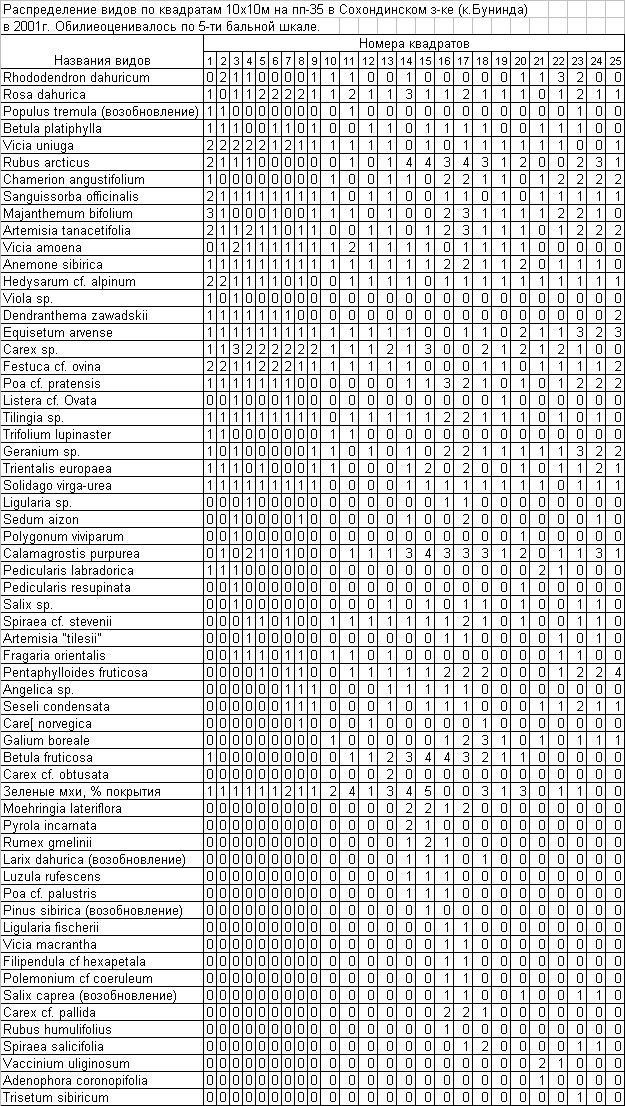Пример В Сохондинском биосферном заповеднике заложена система из 40 постоянных пробных площадей размером 50х50м. На каждой пробной площади проведена таксация древостоя, сделано описание всех синузий проведено картирование древостоя и возобновления. Каждая пробная площадь разбита на 25 квадратов размером 10х10м. Проведено описание растительности на каждом квадрате и результаты сведены в прямоугольную таблицу (см. слева), которая затем анализируется на предмет сходства-различия растительности квадратов. Здесь объекты - растительность квадратов, а признаки - виды растений. В каждом квадрате оценивалось присутствие вида "1", или его отсутствие "0". Для присутствующих видов оценивалось обилие вида по пятибальной шкале. В дальнейшем при расчете попарного сходства растительности квадратов обилие видов не учитывалось, но для каждого вида была расчитана информативность по частоте его встречаемости на квадратах.

Попарное сравнение растительности 25 квадратов в пределах пробной площади позволяет получить матрицу попарного сходства размером 25х25 (см. ниже).

На основе квадратной матрицы бинарного сходства может быть построен граф, который поможет разбить множество объектов на группы (классы) и подгруппы (подклассы), выявить и оценить, таким образом, разнообразие сравниваемых между собой объектов. Это важно при решении задач классификации и ординации сравниваемых объектов, при определении степени дискретности или континуальности разбиения множества этих объектов на группы (классы).

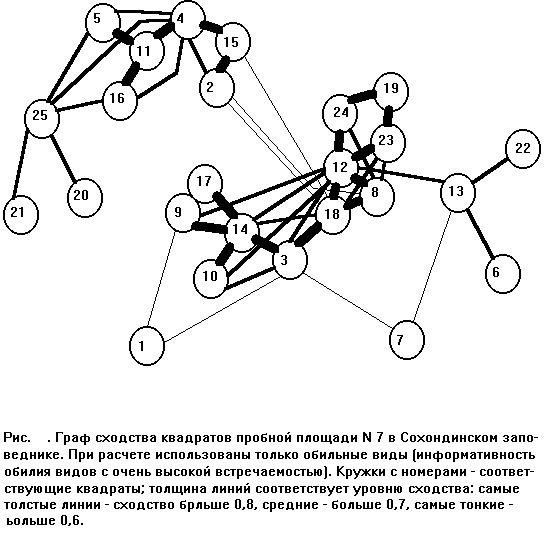Граф представляет собой множество вершин, которые соответствуют сравниваемым объектам. Сходные вершины графа соединены ребрами (линиями), несходные вершины ребрами не соединены. Сходными вершинами считаются такие вершины, сходство которых больше некоторого выбранного уровня (величины). Выбор уровня производится исследователем на основе анализа степени неравномерности графа. Оптимальным считается такой уровень сходства, при котором мы получаем максимально (в данном случае, на данной квадратной матрице) неравномерный граф. Неравномерность графа рассчитывается путем анализа статистического распределения количества вершин графа в зависимости от количества исходящих из этих вершин ребер. При этом эмпирическое распределение сравнивается с распределением теоретическим, построенным исходя из предположения, что все ребра по множеству вершин распределяются случайно. Степень несовпадения эмпирического распределения с рассчитанным теоретически определяется методом Пирсона хи-квадрат. Каждый граф характеризуется количеством вершин, количеством ребер, средним числом ребер на одну вершину, пороговым уровнем сходства, на котором он построен, и степенью неравномерности структуры, оцениваемой величиной хи-квадрат. Оптимальным из множества графов для анализа структуры множества объектов, построенных на основе данной матрицы при разных порогах сходства, мы считаем граф с наибольшим значением хи-квадрат, т.е. наиболее неравномерный граф. Такой граф позволяет выявить большее количество групп (классов) объектов на данном множестве, более тонко проанализировать структуру континуума.   Органицация матрицы проводится графически. Слева: так выглядит один из графов сходства растительности квадратов в пределах постоянной пробной площади.

Более детально суть данного метода описана в наших публикациях (Галанин, 1982, 1989, 1992, Галанин, Беликович, Проскурина, 1986, Беликович, 2001, 2002 и др.). При использовании данного метода ссылка на его автора обязательна. Авторы программы для ПК – А.А. Галанин, А.Г. Есипенко.